Parallel Axis Theorem – Definition, Formula, Derivation & Applications

The Parallel Axis Theorem is a fundamental concept in physics and engineering, especially in the study of rotational dynamics. It allows us to calculate the moment of inertia of a rigid body about any axis, provided we know the moment of inertia about a parallel axis through the center of mass.

Whether you’re designing mechanical parts, analyzing beams in structural engineering, or solving rotational problems in physics, the Parallel Axis Theorem is an essential tool.

What Is the Parallel Axis Theorem?

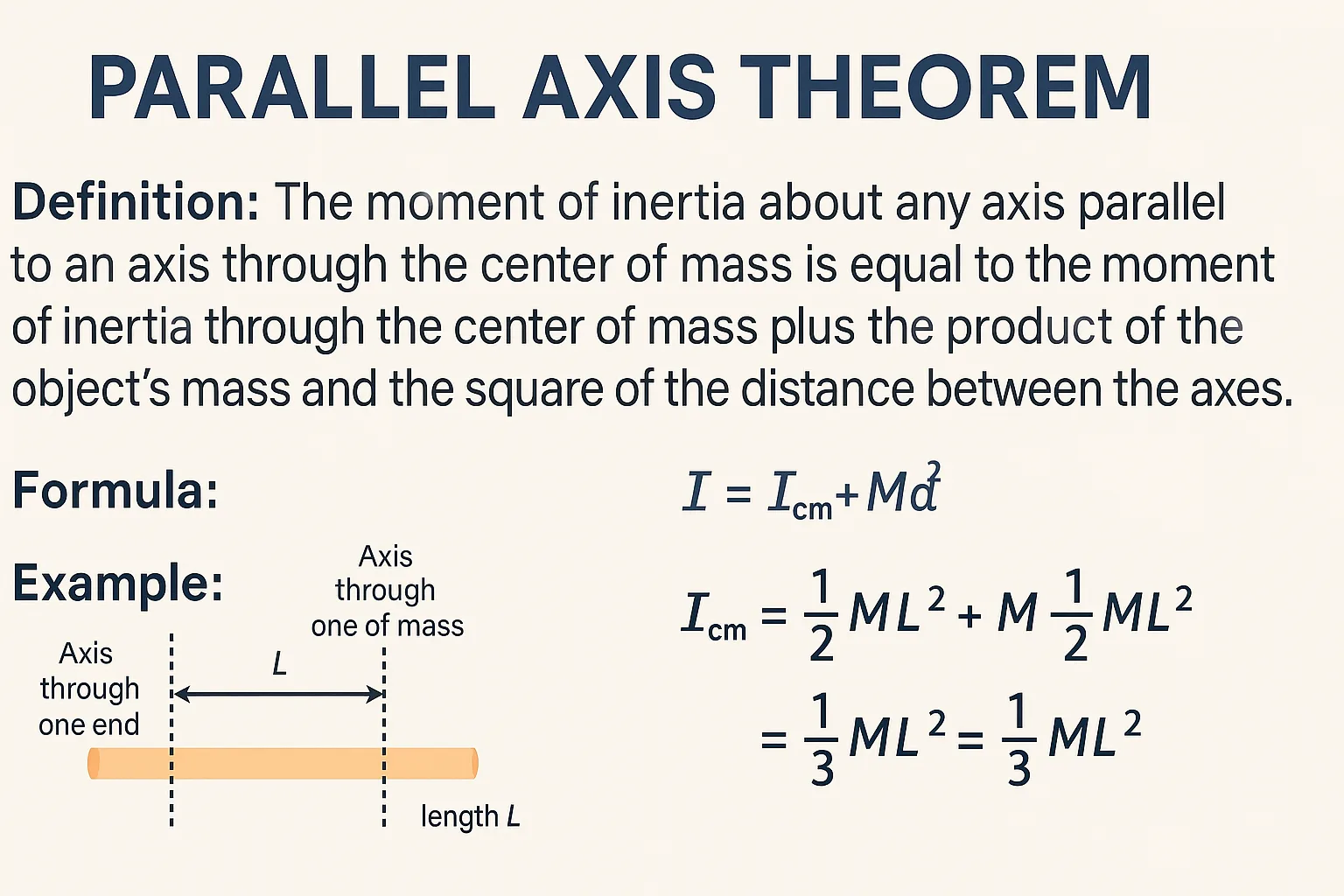
The Parallel Axis Theorem states that the moment of inertia of a body about any axis is equal to the moment of inertia about a parallel axis through the center of mass, plus the product of the object’s mass and the square of the perpendicular distance between the axes.

Parallel Axis Theorem Formula

The formula for the theorem is:

I = I_cm + Md²

Where:

I = Moment of inertia about the new axis

I_cm = Moment of inertia about the center of mass axis

M = Total mass of the object

d = Distance between the center of mass and the new axis

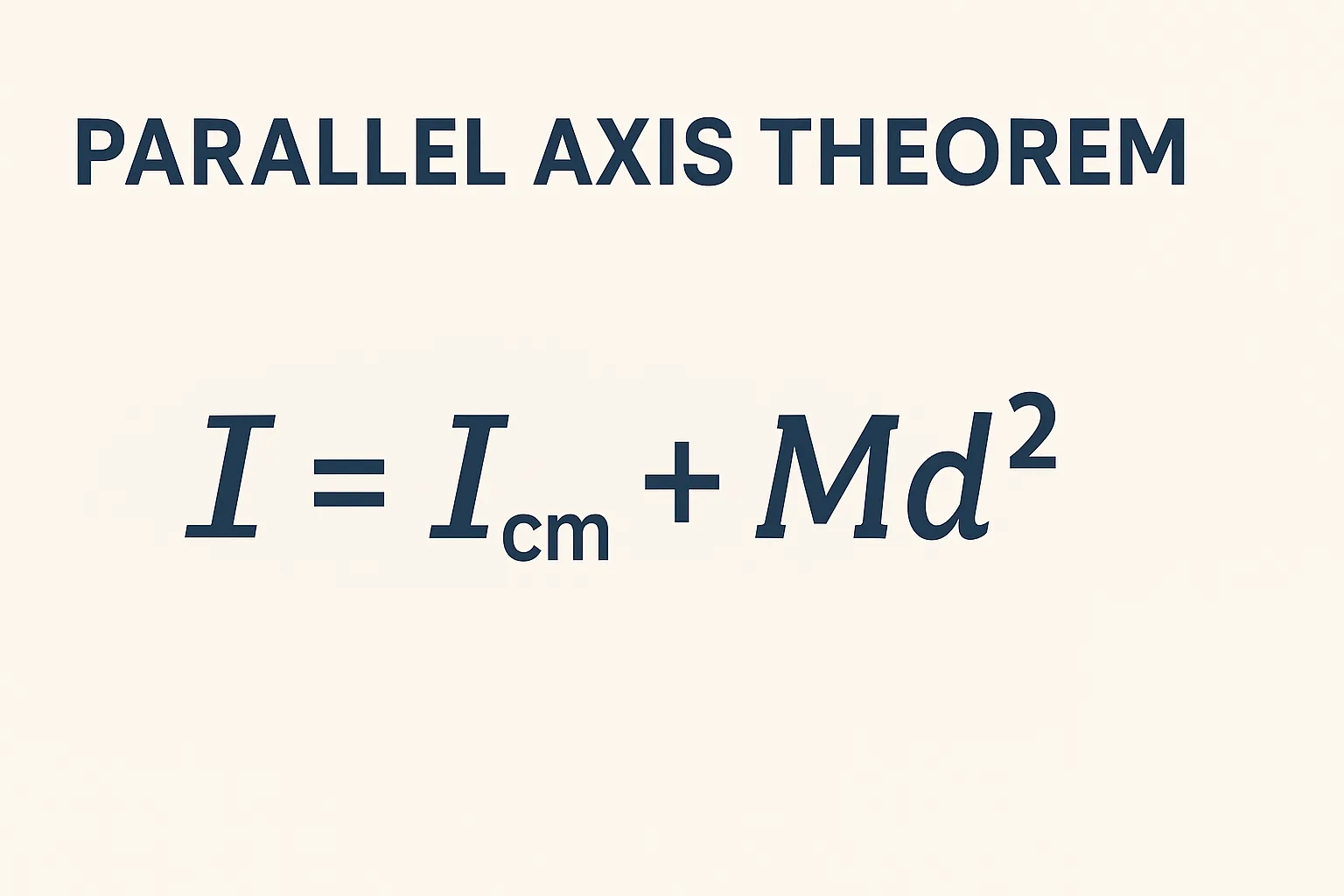
Why Is the Parallel Axis Theorem Important?

In many real-world applications, the axis of rotation is not through the center of mass. Calculating the moment of inertia in such cases directly can be complex. The Parallel Axis Theorem simplifies this process by allowing you to start from the known I_cm and apply a simple correction based on the offset distance.

This is especially useful in:

• Engineering design (e.g., gears, pulleys, beams)
• Robotics (moving arms and parts)
• Aerospace (balancing rotating bodies)
• Physics problems (non-central rotation)

Derivation of the Parallel Axis Theorem (Brief)

Let’s consider a rigid body rotating about an axis at a distance d from its center of mass. If x_cm is the coordinate of the center of mass and x is the coordinate of a mass element dm:

The moment of inertia about the new axis is:

I = ∫ (x + d)² dm
= ∫ x² dm + 2d∫x dm + d²∫dm

Since the integral of x dm over the body is zero (by definition of center of mass), we get:

I = I_cm + Md²

parallel axis theorem moment of inertia

Find the moment of inertia of a uniform rod of mass M and length L about an axis perpendicular to the rod and passing through one end.

Solution:

Moment of inertia through center: I_cm = (1/12)ML²

Distance from center to end: d = L/2

Apply the theorem

I = I_cm + Md²
I = (1/12)ML² + M(L/2)²
I = (1/12)ML² + (1/4)ML²
I = (1/3)ML²

Answer

I = (1/3)ML²

Applications of the Parallel Axis Theorem

Mechanical Engineering – Calculating inertia of rotating components

Civil Engineering – Beam design in structures and bridges

Physics – Solving complex rotation problems

Aerospace – Analyzing satellite and aircraft stability

Robotics – Controlling jointed arms and moving parts

Final Thoughts

The Parallel Axis Theorem is a powerful and practical formula that helps engineers and physicists handle real-world rotational problems with ease. It bridges the gap between ideal models (center of mass rotation) and practical scenarios (off-center axes).

By mastering this concept, you’ll enhance your ability to solve complex rotational motion challenges in both academic and professional environments.